On Math, Music, and the Poetry of Change

For two years since I turned my back on the masters degree program at the Cleveland Institute of Music, I felt as though I'd been stuck in a vicious pirouette, wobbling---NAY---nutating like a dreidel on a narrow outcrop above existential despair. So this past summer I wrenched myself free of Cleveland's desolation in the hope that some ill-advised change would effect a spiritual hard reset. On my second day in Austin, I went to a nearby coffeeshop and happened upon one of my favorite poets, Anis Mojgani, who was working on his laptop in the corner. His raspy "welcome to Austin, best of luck" and the impression of his oddly-shaped hand traced into my notebook were the good omen which validated my decision to move back south.

That said, for the first time since I created this blog in late November of 2012, this is not a post about music. Fuck that. I'm going to write about math.

Frankly, this should have been called Current Obsessions, as it's more true now than ever, but I couldn't relinquish the Shakespeare pun. When my roommate Lyle (AKA lobsterhands) announced that he was starting a degree in Computer Science, I watched over his shoulder as he showed me his code. This toggled in me a primordial boolean switch, causing a long-dormant passion for programming to emerge volcano-like from this teetering bulb of a man, and for the past month, I've spent like, 4-10 hours a day coding. Notably, this is an amount of time I almost never dedicated to cello practice.

Project Euler is a set of mathematical challenges intended to be solved with some sort of computer programming. To begin chipping away at the 400-something problems, I chose to use Ruby, a beautiful object-oriented language designed with readability and productivity in mind, and whose subtleties I have just barely begun to fathom. Many websites (e.g. Hulu) are built on implementations of Ruby.

Late last night I sat down to work out Problem 15:

Lattice Paths. Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner. How many such routes are there through a 20×20 grid?

You're not really supposed to share solutions, but a) this is more of a procedural explanation, b) my way isn't necessarily the quickest or the most intuitive, and besides, c) nobody reads my blog. So I'm going for it. I started by brute forcing my way to find the number of routes through the first few cells, then did some fiddling with formulas to determine the number of possible routes to each intersection in a given row. It looked like this, but messier:

The numbers correspond to the intersection to their bottom-right. Noting also that each intersection was the sum of the intersections above it and to the left---e.g. 35 = (15 + 20), 56 = (21 + 35), etc.---I made a recursive formula to find a given spot, but so many calculations meant it took AGES to come to an answer. Then, at approximately 4 a.m., after a stupid amount of intuition-driven scribbles, I stumbled upon an interesting relationship between any number on the top-right side of the grid and the number diagonally down and left. To find the answer for a 5x5 grid, all one needed to do was make x = 5 * 2, and work your way down and to the left, multiplying like so:

10  * (9/2) = 45  
45  * (8/3) = 120  
120 * (7/4) = 210  
210 * (6/5) = 252  

And that was that. There are 252 possible routes through a 5x5 grid. Thus, a 20x20 (or larger!) grid could be solved by hand:

40  * (39/2) = 780  
780 * (38/3) = 9880  
9880 * (37/4) = 91390  
.
.
.
etc.  

...or by a neat little Ruby program:

def lattice(gridsize)  
  total = gridsize * 2  # sets total at 2 * 20 = 40
  n = (total - 1)       # numerator = 40-1 = 39
  d = 2.to_f            # denominator = 2
  while n > d
    total *= (n / d)    # multiplies total by n / d
    n -= 1
    d += 1
  end
  total.to_i
end

gridsize = 20  
p lattice(gridsize)     # calls function, prints result  

What I later found out is that this problem is basically Pascal's Triangle and my solution is in essence the factorial expression for binomial coefficients:

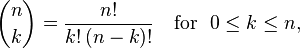
Plugging in 5, we can see that the equations are equal:

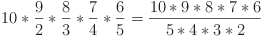
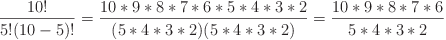
That said, I'm not sure exactly why this works, but it's all pretty neat.

Now, basking in the post-coital contentment of a good math session, I realize that I am a lucky man. As Russell Edson might have said, the last couple years certainly pulled at the difficult head. The shame of quitting was (and is) real, but sometimes change beckons, and with it comes opportunity for salvation. Eventually I stopped spinning and found my balance, and as I backed away from the outcrop, I watched as the land, like Paschal's Triangle, opened up around me, and now suddenly, just as in older times, I am free to roam.

January 30, 2014